Table of Contents
Transient response of second-order circuits
The solutions of all time-dependent circuits look like this:
$$ x(t) = x_p + x_h(t) $$
where $x_p$ is the steady state or particular solution, and $x_h(t)$ is the transient or homogeneous solution. We can get the steady-state solution by replacing capacitors with opens and replacing inductors with shorts, just as in the first-order case. Finding the transient solution takes a bit more effort and is the subject of these notes.
All second-order circuits (in fact, all second-order systems) have characteristic polynomials of the following form:
$$ s^2 + 2 \alpha s + \omega_0^2 $$
- $\alpha$ is the rate of exponential decay.
- $\omega_0$ is the undamped oscillation frequency.
| Series RLC circuit | Parallel RLC circuit | |
|---|---|---|
| $\alpha$ | $\frac{R}{2L}$ | $\frac{1}{2RC}$ |
| $\omega_0$ | $\frac{1}{\sqrt{LC}}$ | $\frac{1}{\sqrt{LC}}$ |
The roots of this characteristic polynomial are:
$$ s = -\alpha \pm \sqrt{\alpha^2 - \omega_0^2} $$
From the roots, it follows that:
- If $\alpha > \omega_0$, the system is overdamped - there will be no oscillations.
- If $\alpha = \omega_0$, the system is critically damped - this is the smallest amount of damping that results in no oscillations.
- If $\alpha < \omega_0$, the system is underdamped, and the output will oscillate while decaying.
| Damping type | Condition | Form of transient solution |
|---|---|---|
| Overdamped | $\alpha \gt \omega_0$ | $ A e^{s_1 t} + B e^{s_2 t} $ where $s_1 = -\alpha + \sqrt{\alpha^2 - \omega_0^2}$ and $s_1 = -\alpha - \sqrt{\alpha^2 - \omega_0^2}$ |
| Critically damped | $\alpha = \omega_0$ | $ A e^{-\alpha t} + B t e^{-\alpha t} $ |
| Underdamped | $\alpha \lt \omega_0$ | $ e^{-\alpha t} [ A \mathrm{cos} (\omega_d t) + B \mathrm{sin} (\omega_d t) ] $ where $ \omega_d = \sqrt{\omega_0^2 - \alpha^2} $ |
Characteristic impedance
The characteristic impedance $Z_0$ is the ratio of the peak capacitor voltage to the peak inductor current:
$$ Z_0 = \frac{v_{peak,C}}{i_{peak,L}} $$
It should not be confused with impedance.
In terms of component values, the characteristic impedance is given by:
$$ Z_0 = \sqrt{\frac{L}{C}} $$
Quality factor
In the time domain, the quality factor is approximately the number of times an underdamped circuit will oscillate before the peaks decay to 4% of the starting values. In terms of component values, it can be expressed as:
$$ Q = \frac{\omega_0}{2\alpha} $$
Finding the transient response
In one common type of problems, we are given a second-order circuit and are asked to find an expression for the transient response of the output of that circuit to some change in the input.
- The first step is to identify the circuit topology and choose the correct expressions for exponential decay rate $\alpha$ and undamped oscillation frequency $\omega_0$
- Then, determine whether the circuit is overdamped, critically damped, or underdamped. We can then write the form of solutions for the output. This form will have 2 unknowns that we need to solve for with 2 initial conditions.
- Find 2 initial conditions. The initial value (e.g. $v(0^+)$ or $i(0^+)$) and the initial first time-derivative (e.g. $\left.\frac{dv}{dt}\right|_{t=0^+}$ or $\left.\frac{di}{dt}\right|_{t=0^+}$) of the output will work.
- Finally, use the initial conditions to find the coefficients in the solution.
Example (from Final Exam Practice Set 1)
The figure below shows a parallel RLC circuit driven by a current source. The circuit parameters are $L = 1 \mu H$, $C = 1 \mu F$, $R = 1 \Omega$, $I = 1 A$. The switch is closed for $t < 0$, and it opens permanently at $t = 0$. (You may assume that the inductor current is zero at $t = 0_–$.) Find $v(t)$ for $t > 0$.
First, let's find the steady-state or particular solution. We can see that if we replace the capacitor with an open and the inductor with a short, the voltage $v(t)$ will be $0$. Therefore, the steady-state solution is:
$$v_p = 0$$
Now let's find the transient solution. Clearly, this is a parallel RLC circuit. That means that for this circuit:
- $\alpha = \frac{1}{2RC} = \frac{1}{2(1 \Omega)(1 \mu F)} = 5 \times 10^5 rad/s $
- $\omega_0 = \frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{(1 \mu H)(1 \mu F)}} = 10^6 rad/s$
Since $\alpha < \omega_0$, this circuit is underdamped.
That means our homogeneous solution will be of the form:
$$ v_h(t) = e^{-\alpha t} [ A \mathrm{cos} (\omega_d t) + B \mathrm{sin} (\omega_d t) ] $$
And the total solution, including the particular solution, is:
$$ v(t) = v_p(t) + v_h(t) = 0 + e^{-\alpha t} [ A \mathrm{cos} (\omega_d t) + B \mathrm{sin} (\omega_d t) ] $$
where
- $\alpha = 5 \times 10^5 rad/s$
- $\omega_d = \sqrt{\omega_0^2 - \alpha^2} = \sqrt{(10^6)^2 - (5 \times 10^5)^2} = 8.66 \times 10^5 rad/s$
Let's find the initial conditions. First, we can find the initial value of the solution. Since $v_c(0^+) = v_c(0^-)$ and $v_c(0^-) = 0$ (because it was shorted),
$$v(0^+) = v_c(0^+) = 0$$
Next, we can find the initial value of the time derivative of the solution $\left.\frac{dv}{dt}\right|_{t = 0^+}$.
The constitutive relation of the capacitor, $i_C = C \frac{dv_C}{dt}$, can give us this time derivative.
Because $v(0^+) = 0$, $i_R(0^+) = \frac{v(0^+)}{R} = 0$. And because $i_L(0^+) = i_L(0^-)$ and $i_L(0^-) = 0$ (given),
$$i_L(0^+) = 0$$
Therefore, all of the current from the current source is flowing into the capacitor at time $t = 0^+$:
$$i_C(0^+) = I$$
So,
$$\left.\frac{dv}{dt}\right|_{t = 0^+} = \left.\frac{dv_C}{dt}\right|_{t = 0^+} = \frac{i_C(0^+)}{C} = \frac{I}{C}$$
Let's now find coefficients $A$ and $B$ that satisfy these initial conditions.
Starting with the $v(0^+) = 0$ condition:
$$ e^{-\alpha (0)} [ A \mathrm{cos} (\omega_d (0)) + B \mathrm{sin} (\omega_d (0)) ] = 0 $$
$$ A = 0 $$
Now we know that:
$$ v(t) = B e^{-\alpha t} \mathrm{sin} (\omega_d t) $$
Let's now use the condition $\left.\frac{dv}{dt}\right|_{t = 0^+} = \frac{I}{C}$ condition. We have to take the derivative of $v(t)$:
$$ \frac{dv}{dt} = -B \alpha e^{-\alpha t} \mathrm{sin} (\omega_d t) + B e^{-\alpha t} \omega_d \mathrm{cos} (\omega_d t) $$
Plug in $t = 0^+$:
$$ \left.\frac{dv}{dt}\right|_{t = 0^+} = -B \alpha e^{-\alpha (0)} \mathrm{sin} (\omega_d (0)) + B e^{-\alpha (0)} \omega_d \mathrm{cos} (\omega_d (0)) $$
$$ \left.\frac{dv}{dt}\right|_{t = 0^+} = B \omega_d $$
Equate the expression for $\left.\frac{dv}{dt}\right|_{t = 0^+}$ to the initial condition we found earlier.
$$ B \omega_d = \frac{I}{C} $$
$$ B = \frac{I}{C \omega_d} $$
Therefore, our solution is:
$$ v(t) = \frac{I}{C \omega_d} e^{-\alpha t} \mathrm{sin} (\omega_d t) $$
We can plug in numbers:
$$ v(t) = \frac{1 A}{(1 \mu F)(8.66 \times 10^5 rad/s)} e^{-(5 \times 10^5 rad/s) t} \mathrm{sin} ((8.66 \times 10^5 rad/s)t) $$
Finding component values given a plot
Another common type of problems gives us a plot of a transient response of an RLC circuit and asks us to find the values of components in the circuit.
If we are given a plot of a transient response, we can extract the following information:
- Decay rate $\alpha$
- Damped oscillation frequency $\omega_d$
$\omega_d$ is straightforward to extract. We can just consider the time between two adjacent peaks (or troughs) as the “period” $T$ (in scare quotes because this signal is technically not periodic) and then divide $2\pi$ by the period:
$$ \omega_d = \frac{2\pi}{T} $$
$\alpha$ can also be extracted from a plot. Consider two adjacent peaks, which occur at times $t_1$ and $t_2$ and have magnitudes $x_1$ and $x_2$. Then, the exponential decay can be calculated by:
$$ \frac{x_2}{x_1} = \frac{e^{-\alpha t_2}}{e^{-\alpha t_1}} $$
$$ \frac{x_2}{x_1} = e^{-\alpha (t_2 - t_1)} $$ $$ \ln{\frac{x_2}{x_1}} = -\alpha (t_2 - t_1) $$ $$ \alpha = -\frac{\ln{\frac{x_2}{x_1}}}{t_2 - t_1} $$
From $\alpha$ and $\omega_d$ we can also find $\omega_0$:
$$ \omega_0 = \sqrt{\omega_d^2 + \alpha^2} $$
With this information, we can equate $\alpha$ and $\omega_0$ to the expressions in terms of component values, which are shown in the table above.
Example (adapted from Final Exam Practice Set 1)
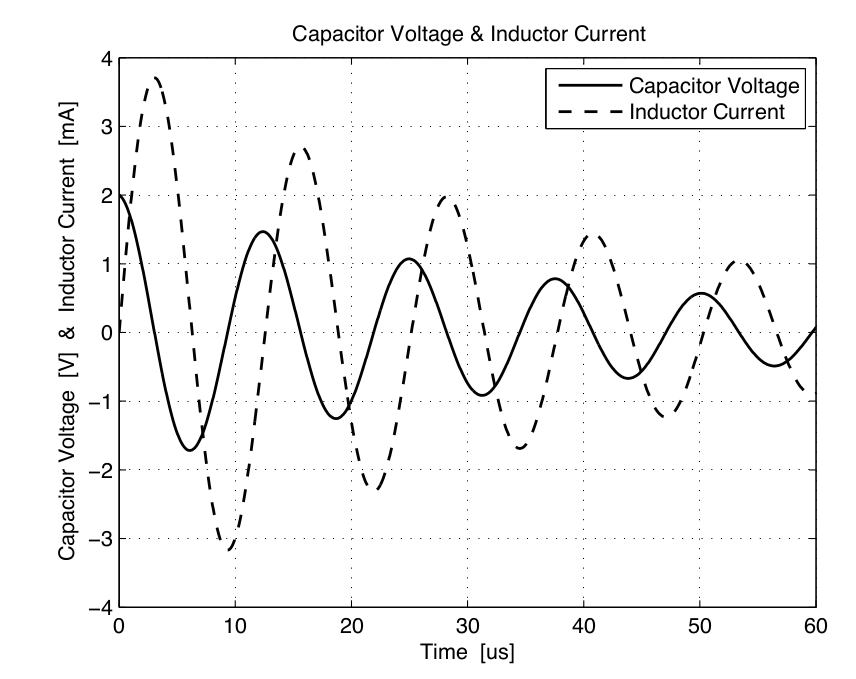
This problem concerns the second-order network shown below. To begin, the connection between the voltage source and the capacitor is broken, and the capacitor is connected to the RL circuit in parallel. A graph of the subsequent capacitor voltage v in volts and inductor current i in milliamps is also shown below as a function of time in microseconds. What are the approximate values of R, L, C, and the quality factor Q?
Let's start with the easiest value to extract, which is the damped frequency $\omega_d$. If we look at the capacitor voltage, we can see that there is a peak at $(0us, 2V)$ and another one at $(12.5us, 1.5V)$. So the damped frequency is:
$$ \omega_d = \frac{2\pi}{12.5us - 0us} = 5.027 \times 10^5 rad/s $$
Now onto damping $\alpha$. We can again look at the two peaks $(0us, 2V)$ and $(12.5us, 1.5V)$. The formula for calculating $\alpha$ is:
$$ \alpha = -\frac{\ln{\frac{x_2}{x_1}}}{t_2 - t_1} $$
We can plug in our values:
$$ \alpha = -\frac{\ln{\frac{1.5}{2}}}{12.5us - 0} = 2.3 \times 10^4 rad/s$$
Undamped frequency is therefore:
$$ \omega_0 = \sqrt{\omega_d^2 + \alpha^2} = 5.032 \times 10^5 rad/s $$
Because this is a parallel RLC circuit, we know that:
$$ \alpha = \frac{1}{2RC} = 2.3 \times 10^4 rad/s $$ $$ \omega_0 = \frac{1}{\sqrt{LC}} = 5.032 \times 10^5 rad/s $$
We now have two equations for three unknowns. The third equation will come from solving for and using the characteristic impedance.
$$ Z_0 = \frac{v_{peak,C}}{i_{peak,L}} \approx \frac{2V}{3.75mA} = 533.3 \Omega $$
$$ Z_0 = \sqrt{\frac{L}{C}} = 533.3 \Omega $$
Using these three equations, we can solve for R, L, and C:
$$ R = 6.702 \times 10^3 \Omega $$ $$ L = 1.061 \times 10^{-3} H $$ $$ C = 3.730 \times 10^{-9} F $$
And quality factor Q is:
$$ Q = \frac{\omega_0}{2\alpha} = 12.57 $$